Что такое Глубокое Обучение и как оно работает? Объяснение для начинающих от Digimagg

Что такое глубокое обучение?

Глубокое обучение, разновидность машинного обучения, черпает вдохновение из архитектуры человеческого мозга. Его алгоритмы направлены на имитацию человеческого мышления путем систематического анализа данных с использованием заранее определенных логических рамок. Этому способствуют нейронные сети, состоящие из многоуровневых алгоритмов.

Глубокое обучение подпадает под действие машинного обучения, которое, в свою очередь, является компонентом искусственного интеллекта. Искусственный интеллект включает в себя методы, позволяющие компьютерам имитировать поведение человека. Для достижения этой цели машинное обучение включает в себя алгоритмы, обученные на данных. Глубокое обучение, вдохновленное структурой человеческого мозга, представляет собой особую форму машинного обучения.

Как работает глубокое обучение?

Алгоритмы глубокого обучения стремятся получить информацию, сопоставимую с человеческими рассуждениями, путем непрерывного анализа данных, структурированных определенным образом. Этому способствует использование нейронных сетей, которые содержат несколько уровней алгоритмов.

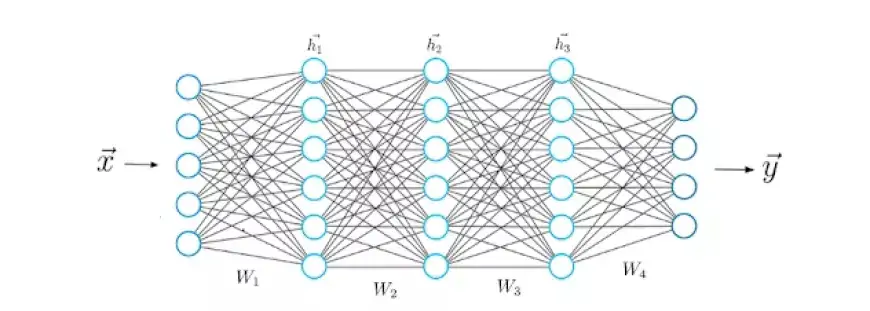
Архитектура нейронных сетей вдохновлена ​​структурой человеческого мозга. Точно так же, как люди используют свой мозг для распознавания закономерностей и классификации различных типов информации, нейронные сети можно научить выполнять аналогичные задачи с данными.

Каждый уровень нейронных сетей можно рассматривать как фильтр, который работает постепенно от грубого к сложному, тем самым повышая вероятность получения точных результатов. Это отражает работу человеческого мозга, который сравнивает поступающую информацию с существующими знаниями. Глубокие нейронные сети используют тот же принцип.

Нейронные сети позволяют решать множество задач, таких как кластеризация, классификация и регрессия. Они могут группировать или систематизировать немаркированные данные на основе сходства между выборками или классифицировать выборки по разным группам, используя маркированные наборы данных.

По сути, нейронные сети могут выполнять задачи, аналогичные классическим алгоритмам машинного обучения, но обратное неверно. Искусственные нейронные сети обладают уникальными возможностями, которые позволяют моделям глубокого обучения решать задачи, недоступные традиционным моделям машинного обучения.

Значительные успехи в области искусственного интеллекта, наблюдаемые в последние годы, объясняются глубоким обучением. Без этого не было бы таких достижений, как беспилотные автомобили, чат-боты и виртуальные помощники, такие как Alexa и Siri. Google Translate останется на зачаточном уровне, а у Netflix не будет персонализированных рекомендаций. Нейронные сети лежат в основе всех этих приложений и технологий глубокого обучения.

Промышленная революция, подпитываемая искусственными нейронными сетями и глубоким обучением, уже идет. В конечном счете, глубокое обучение является наиболее эффективным и очевидным способом достижения настоящего машинного интеллекта.

Что делает глубокое обучение столь широко распространенным?

Нет извлечения функций

Одно из основных преимуществ глубокого обучения по сравнению с машинным обучением заключается в устранении необходимости ручного извлечения признаков, также известного как разработка признаков.

До появления глубокого обучения обычно использовались традиционные методы машинного обучения, такие как деревья решений, SVM, наивный байесовский классификатор и логистическая регрессия. Эти алгоритмы, часто называемые «плоскими» алгоритмами, требуют этапа предварительной обработки, известного как извлечение признаков, прежде чем их можно будет применить непосредственно к необработанным данным, таким как файлы .csv, изображения или текст.

Извлечение признаков включает преобразование необработанных данных в представление, которое эти классические алгоритмы машинного обучения могут использовать для выполнения таких задач, как классификация по различным категориям или классам. Этот этап предварительной обработки обычно сложен и требует глубокого понимания проблемной области. Для достижения оптимальных результатов требуется адаптация, тестирование и доработка в течение нескольких итераций.

Напротив, искусственные нейронные сети глубокого обучения обходят необходимость извлечения признаков. Уровни в этих сетях имеют возможность автономно изучать непосредственно неявное представление необработанных данных.

Вот механизм: через несколько слоев искусственной нейронной сети генерируется все более абстрактное и сжатое представление необработанных данных. Это сжатое представление входных данных затем используется для получения желаемого результата, например, для классификации входных данных на отдельные классы.

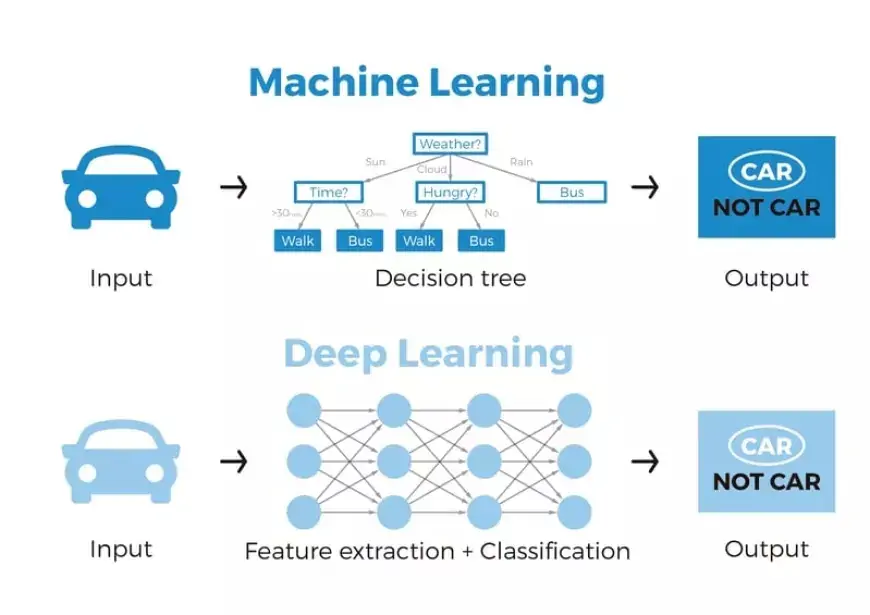
По сути, процесс извлечения признаков по своей сути интегрирован в работу искусственной нейронной сети.

На этапе обучения нейронная сеть настраивает этот процесс для получения наиболее оптимального абстрактного представления входных данных. Следовательно, модели глубокого обучения требуют минимального ручного вмешательства для выполнения и уточнения процедуры извлечения признаков.

Для иллюстрации предположим, что мы хотим использовать модель машинного обучения, чтобы определить, изображает ли данное изображение автомобиль или нет. Традиционно люди должны сначала идентифицировать отличительные особенности автомобиля (например, форму, размер, окна, колеса и т. д.), извлечь эти характеристики и предоставить их алгоритму в качестве входных данных. Впоследствии алгоритм выполняет классификацию изображений. По сути, в машинном обучении прямое вмешательство программиста необходимо для того, чтобы модель пришла к выводу.

Однако в контексте модели глубокого обучения этап извлечения признаков становится устаревшим. Модель по своей сути распознает эти уникальные характеристики автомобиля и точно прогнозирует результаты без вмешательства человека.

Фактически, отказ от явного извлечения признаков применим к каждой задаче, выполняемой с помощью нейронных сетей. Просто предоставьте необработанные данные в нейронную сеть, а модель самостоятельно обработает все остальное.

Повышение точности глубокого обучения с помощью больших данных

Еще одним значительным преимуществом глубокого обучения, которое подчеркивает его растущую популярность, является его зависимость от огромных объемов данных. Эра больших данных открывает огромные возможности для инноваций в глубоком обучении. Эндрю Нг, главный научный сотрудник Baidu, известной поисковой системы в Китае, соучредитель Coursera и ключевая фигура в проекте Google Brain Project, метко сравнивает ИИ со строительством ракетного корабля. Он утверждает:

«Я думаю, что искусственный интеллект сродни созданию ракетного корабля. Вам нужен огромный двигатель и много топлива. Если у вас большой двигатель и крошечное количество топлива, вы не доберетесь до орбиты. Если у вас крошечный двигатель и тонна топлива, вы даже не сможете взлететь. Чтобы построить ракету, нужен огромный двигатель и много топлива».

В контексте глубокого обучения ракетный двигатель символизирует модели глубокого обучения, а топливо представляет собой огромные объемы данных, которые можно ввести в эти алгоритмы.

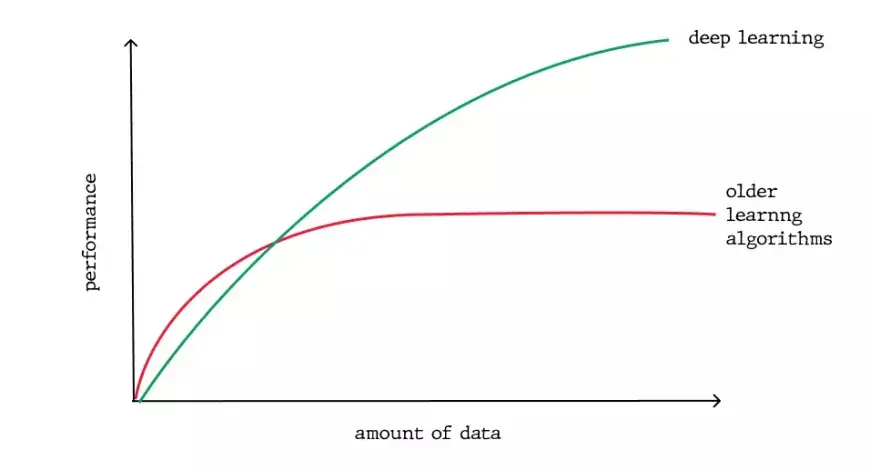
Модели глубокого обучения обычно повышают свою точность, поскольку они обучаются на более крупных наборах данных, в отличие от традиционных моделей машинного обучения, таких как SVM и наивный байесовский классификатор, улучшение которых прекращается после достижения точки насыщения.

Как работают нейронные сети глубокого обучения?

Искусственные нейронные сети

Теперь, когда у нас есть фундаментальное понимание функционирования биологических нейронных сетей, давайте углубимся в структуру искусственных нейронных сетей.

Искусственная нейронная сеть обычно состоит из взаимосвязанных блоков или узлов, называемых нейронами. Эти искусственные нейроны созданы на основе биологических нейронов нашего мозга.

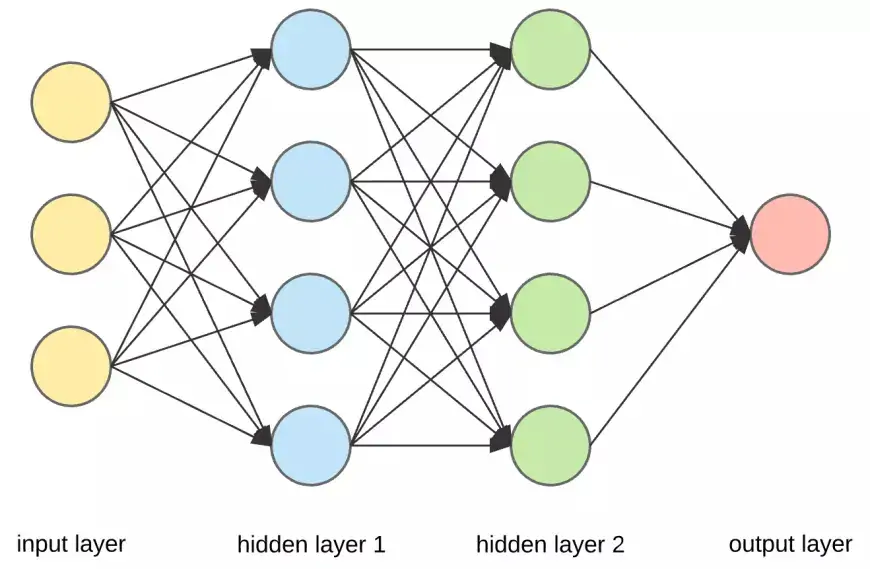
Нейрон служит визуальным представлением числового значения (например, 1,2, 5,0, 42,0, 0,25 и т. д.). В контексте биологического мозга любую связь между двумя искусственными нейронами можно сравнить с аксоном. Эти связи между нейронами устанавливаются посредством весов, которые по сути являются числовыми значениями.

В процессе обучения искусственной нейронной сети эти веса между нейронами подвергаются корректировке, влияющей на прочность связей. Но что это влечет за собой? При предоставлении обучающих данных и конкретной задачи, такой как классификация чисел, цель состоит в том, чтобы определить конкретный набор весов, которые позволят нейронной сети выполнить классификацию.

Набор весов варьируется для каждой задачи и набора данных. Заранее предвидеть точные значения этих весов непрактично; вместо этого нейронная сеть должна их изучить. Этот процесс приобретения знаний известен как обучение.

Биологические нейронные сети

Искусственные нейронные сети черпают вдохновение из структуры биологических нейронов, присутствующих в человеческом мозге. Эти искусственные аналоги имитируют некоторые фундаментальные аспекты биологических нейронных сетей, хотя и в упрощенной форме. Чтобы получить представление об искусственных нейронных сетях, полезно изучить структуру биологических нейронных сетей.

По сути, биологическая нейронная сеть состоит из множества нейронов.

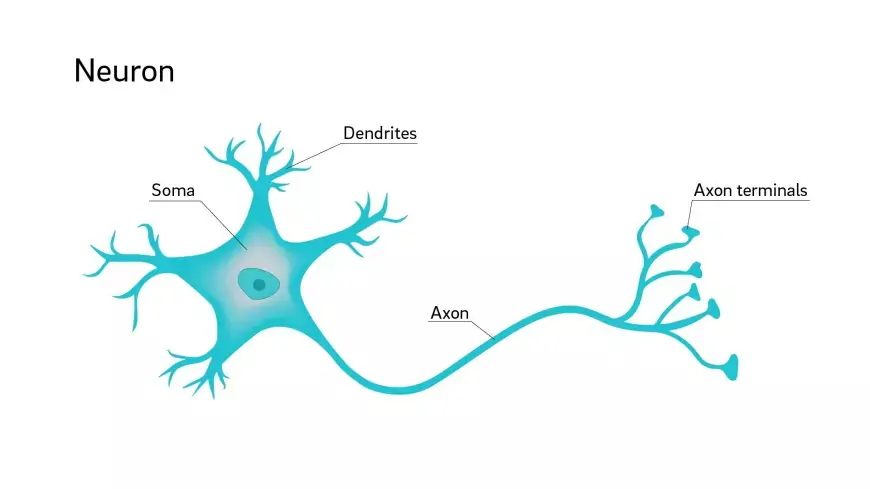
Соединения слоев в нейронной сети глубокого обучения

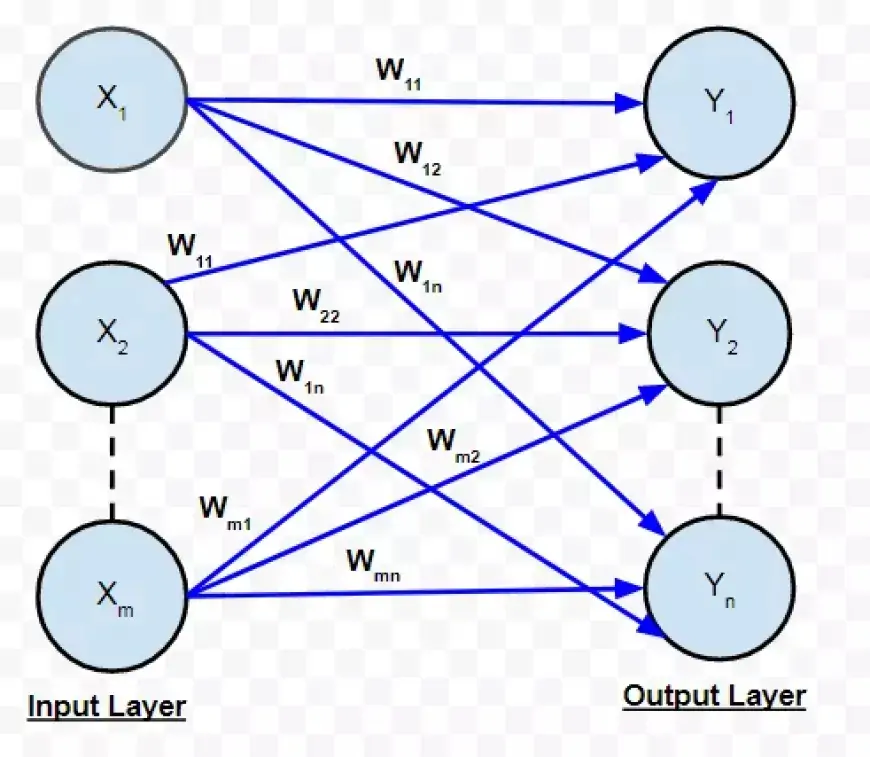
Давайте рассмотрим упрощенную нейронную сеть всего с двумя слоями. Входной слой содержит два нейрона, а выходной слой — три нейрона.

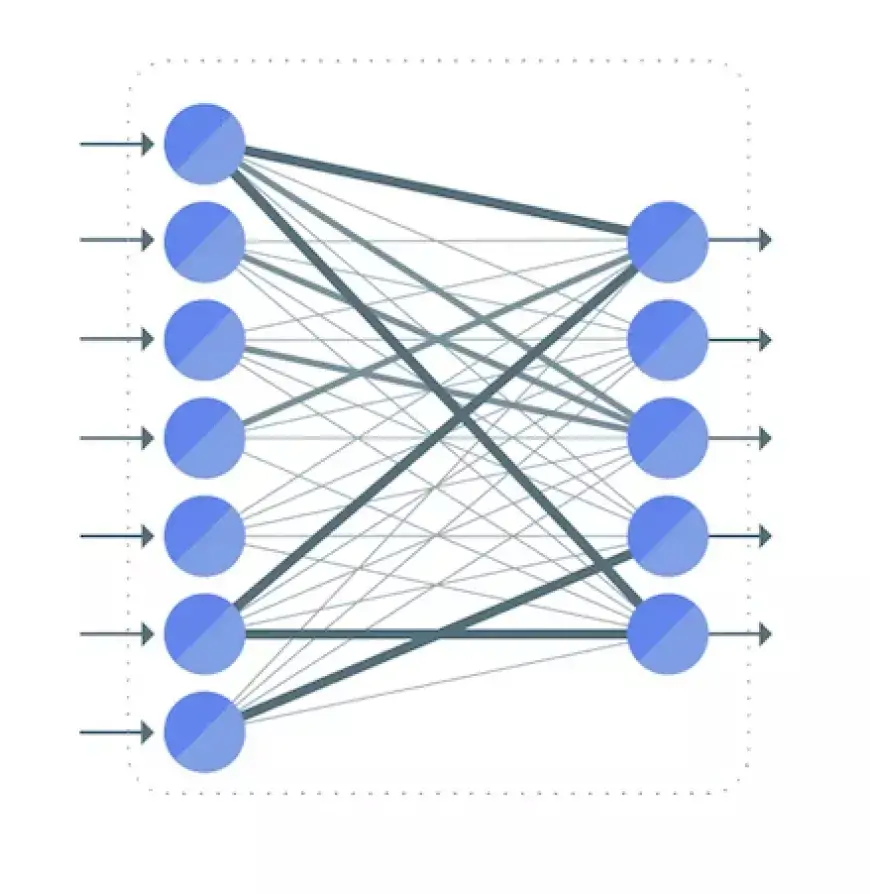
Как обсуждалось ранее, связь между двумя нейронами обозначается числовым значением, известным как вес.

На иллюстрации каждому соединению между двумя нейронами присвоен отдельный вес, представленный символом «w». Эти веса индексируются: первое значение указывает количество нейронов в слое, из которого возникает соединение, а второе значение указывает количество нейронов в слое, к которому ведет соединение.

Все веса между слоями нейронной сети могут быть инкапсулированы в матрицу, называемую матрицей весов.

Матрица весов содержит то же количество элементов, что и общее количество связей между нейронами. Его размеры определяются размерами двух слоев, связанных этой матрицей.

Количество строк соответствует количеству нейронов в слое, из которого происходят соединения, а количество столбцов соответствует количеству нейронов в слое, к которому ведут соединения.

В этом конкретном случае строки весовой матрицы соответствуют размеру входного слоя, равному двум, а ее столбцы соответствуют размеру выходного слоя, равному трем.

Архитектура нейронной сети глубокого обучения

В стандартной структуре нейронной сети имеется несколько слоев, первый из которых называется входным слоем. Этот уровень получает входные данные, обозначенные как x, которые содержат данные, на которых обучается нейронная сеть. Например, в нашем более раннем сценарии классификации рукописных чисел эти входные данные x будут соответствовать изображениям этих чисел. По сути, x — это полный вектор, где каждая запись представляет пиксель.

Входной слой содержит столько же нейронов, сколько элементов в векторе x. По сути, каждый входной нейрон соответствует одному элементу вектора.

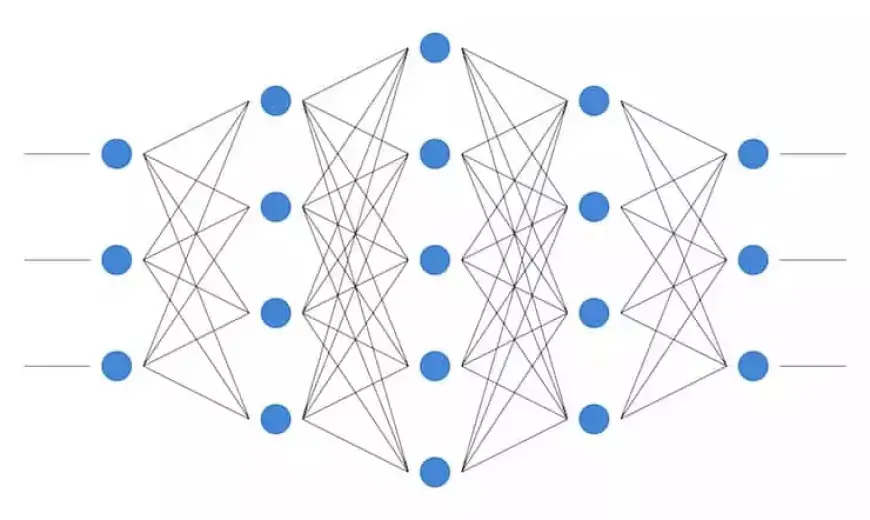
Последний слой, известный как выходной слой, создает вектор y, который представляет результат работы нейронной сети. Каждая запись в этом векторе соответствует значениям активации нейронов выходного слоя. В контексте задач классификации каждый нейрон в этом последнем слое обозначает отдельный класс.

В этом сценарии значение активации выходного нейрона указывает на вероятность того, что входные признаки x, обычно представляющие рукописную цифру, принадлежат определенному классу (например, одной из цифр 0–9). Важно убедиться, что количество выходных нейронов соответствует количеству отдельных классов.

Чтобы сгенерировать вектор прогнозирования y, сеть подвергается различным математическим операциям внутри скрытых слоев, расположенных между входным и выходным слоями. Эти промежуточные уровни облегчают преобразование входных данных в значимые выходные прогнозы. Теперь углубимся в структуру связей между этими слоями.

Функции потерь в глубоком обучении

Как только нейронная сеть сгенерирует свой прогноз, необходимо сопоставить этот вектор прогнозирования с фактической меткой основной истины, обозначенной как y_hat.

Хотя вектор y представляет собой прогнозы, вычисленные нейронной сетью во время прямого распространения, которые могут значительно отличаться от истинных значений, y_hat содержит фактические значения.

Математически мы оцениваем несоответствие между y и y_hat, устанавливая функцию потерь, величина которой зависит от этого несоответствия.

Примером общей функции потерь является квадратичная потеря:

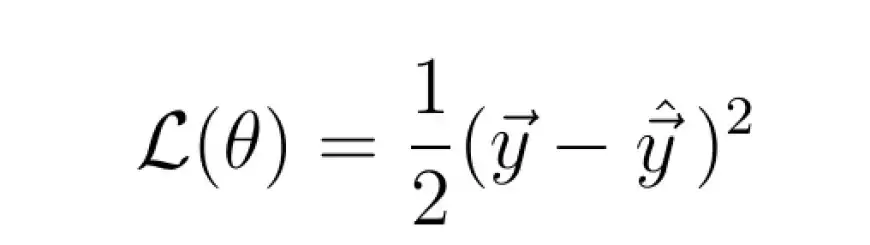
Величина функции потерь зависит от различия между y_hat и y. Большая разница приводит к более высокому значению потерь, тогда как меньшая разница приводит к более низкому значению потерь.

Непосредственная минимизация функции потерь приводит к повышению точности прогнозов нейронной сети, поскольку уменьшает несоответствие между прогнозом и фактической меткой.

Минимизируя функцию потерь, модель нейронной сети автоматически улучшает свою прогнозирующую производительность независимо от конкретных характеристик решаемой задачи. Ключ заключается в выборе подходящей функции потерь для задачи.

К счастью, для большинства практических задач необходимы только две основные функции потерь: потеря перекрестной энтропии и потеря среднеквадратической ошибки (MSE).

Потеря перекрестной энтропии

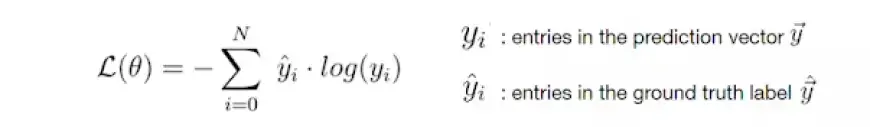
Среднеквадратическая потеря ошибки

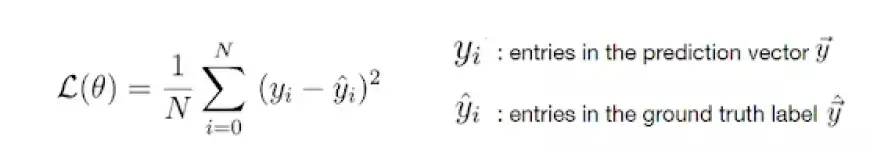
Поскольку на потери влияют веса, необходимо найти определенную комбинацию весов, которая минимизирует функцию потерь. Этот процесс оптимизации осуществляется математически с использованием метода, известного как градиентный спуск.

Изучение процесса нейронной сети глубокого обучения

Имея более четкое представление о структуре нейронной сети, мы можем систематически углубиться в процесс обучения. Давайте разберем это шаг за шагом. На начальном этапе, с которым вы уже знакомы, нейронная сеть вычисляет вектор прогнозирования, обозначенный как h, для заданного входного вектора признаков x.

Этот шаг обычно называют прямым распространением. Это влечет за собой использование входного вектора x и весовой матрицы W, которая соединяет два слоя нейронов, для вычисления скалярного произведения между x и W. Результатом этого скалярного произведения является еще один вектор, обозначенный как z.

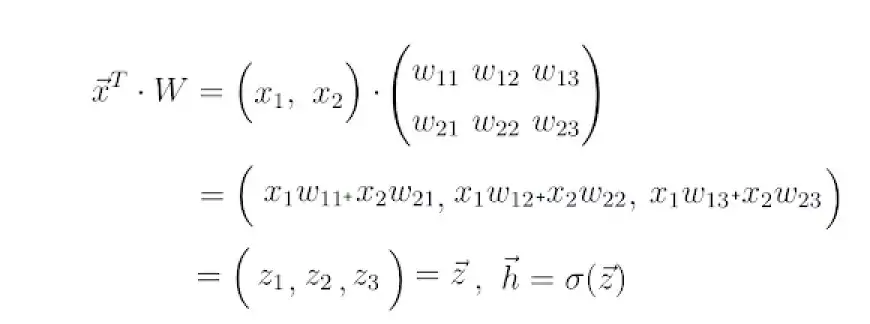
Конечный вектор прогнозирования, обозначаемый как h, получается путем применения функции активации, часто обозначаемой символом сигма, к вектору z. Эта функция активации служит нелинейным отображением z в h.

В глубоком обучении обычно используются три функции активации: tanh, сигмовидная и ReLU.

На этом этапе становится очевидным, что нейроны в нейронной сети просто представляют числовые значения. Давайте на мгновение внимательно рассмотрим вектор z.

Каждый элемент z содержит входной вектор x. Здесь становится очевидным значение весов. Значение нейрона в слое является результатом линейной комбинации значений нейронов предыдущего слоя, взвешенных по числовым значениям.

Эти числовые значения представляют собой веса, указывающие на силу связей между нейронами.

Во время тренировки эти веса корректируются, в результате чего некоторые нейроны становятся более прочными, а другие — менее. Подобно биологическим нейронным сетям, обучение в искусственных нейронных сетях предполагает изменение весов. Следовательно, значения z, h и конечного выходного вектора y колеблются в зависимости от весов. Некоторые веса приближают предсказания нейронной сети к фактическому вектору истинности y_hat, тогда как другие увеличивают расхождение.

Теперь, имея представление о математических операциях между двумя слоями нейронной сети, мы можем расширить наше понимание и охватить более глубокие архитектуры, состоящие из пяти слоев.

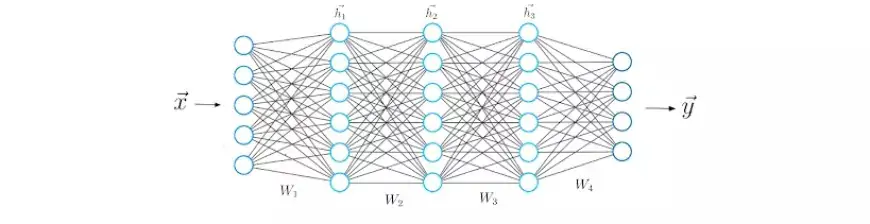
Как и на предыдущем шаге, мы вычисляем скалярное произведение входного вектора x и первой весовой матрицы W1, а затем применяем функцию активации к результирующему вектору, получая первый скрытый вектор h1. Впоследствии мы рассматриваем h1 как входные данные для последующего третьего слоя. Этот процесс повторяется до тех пор, пока мы в конечном итоге не получим окончательный выходной вектор y.

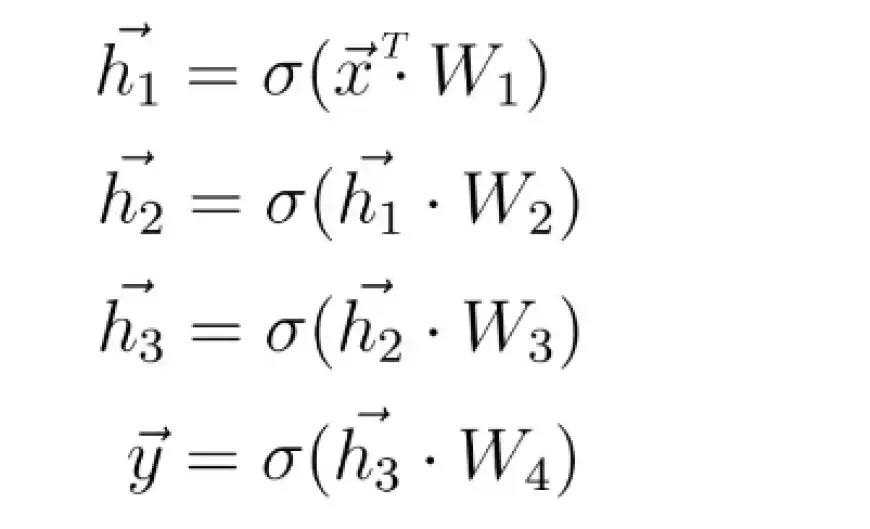
Градиентный спуск в глубоком обучении

В процессе градиентного спуска мы используем градиент функции потерь (по сути, ее производную) для уточнения весов нейронной сети.

Чтобы понять фундаментальную идею градиентного спуска, давайте рассмотрим простой пример нейронной сети, состоящей всего из одного входного и одного выходного нейрона, соединенных весовым значением, обозначенным как w.

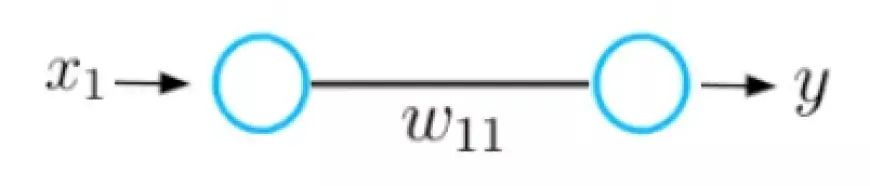
В этой нейронной сети принимается входной сигнал x, а на выходе генерируется прогноз y. Предположим, что начальное значение веса этой нейронной сети равно 5, а входное значение x равно 2. Следовательно, прогноз y этой сети будет равен 10, а метка y_hat может быть равна 6.

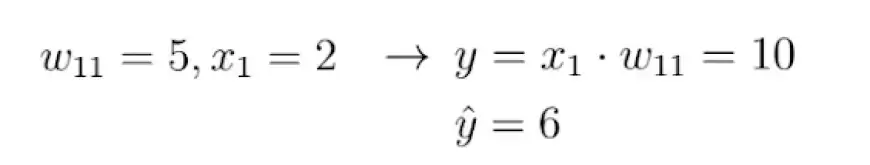
Это указывает на то, что прогноз неточный, что побуждает нас использовать метод градиентного спуска для определения нового значения веса, которое позволит нейронной сети сделать правильный прогноз. В качестве предварительного шага нам необходимо выбрать подходящую для задачи функцию потерь.

Давайте выберем упомянутую ранее квадратичную функцию потерь и визуализируем эту функцию, которая по сути проявляется как квадратичная функция:

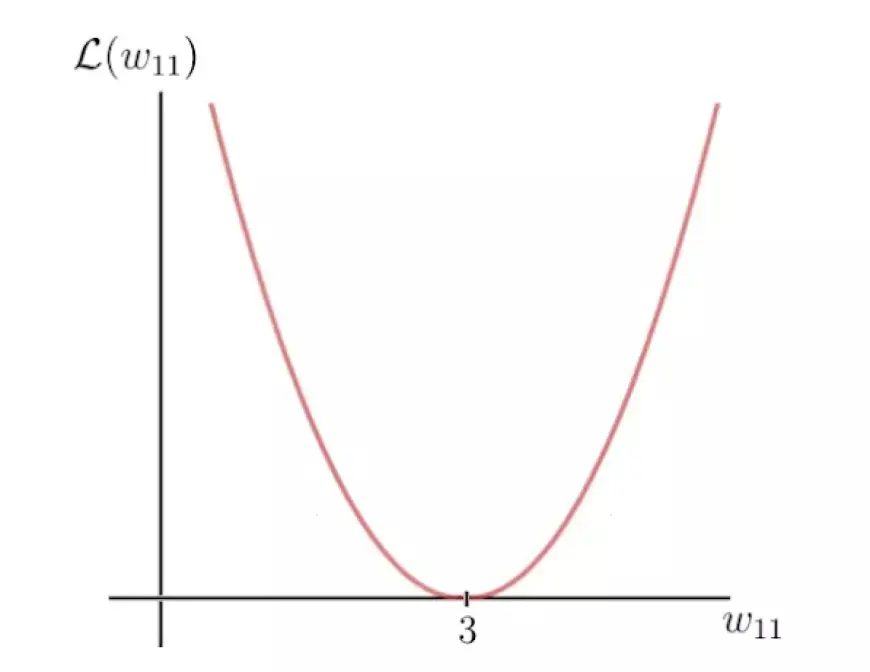
Ось Y обозначает значение потерь, которое зависит от несоответствия между меткой и прогнозом и, следовательно, от параметров сети — в частности, в данном случае от единственного весового параметра w. С другой стороны, ось X представляет диапазон значений этого веса.

Очевидно, что существует определенный вес, обозначаемый как w, при котором функция потерь достигает глобального минимума. Это значение представляет собой оптимальный весовой параметр, который поможет нейронной сети сделать правильный прогноз, который в этом сценарии равен 6. Примечательно, что значение этого оптимального веса идентифицируется как 3.

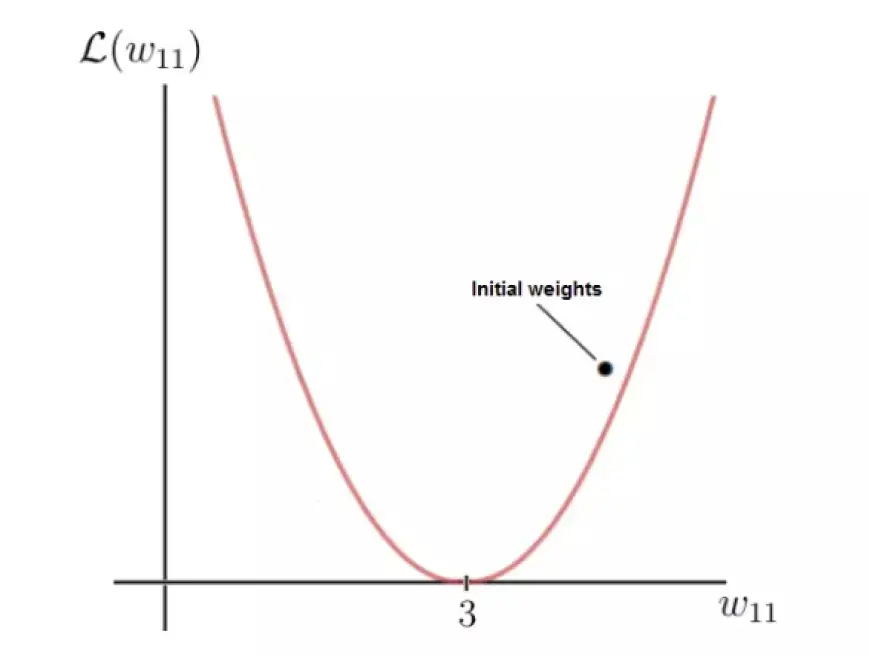
И наоборот, наш стартовый вес 5 приводит к относительно высоким потерям. Теперь цель состоит в том, чтобы итеративно корректировать параметр веса, пока мы не придем к оптимальному значению для этого конкретного веса. Здесь мы используем градиент функции потерь.

К счастью, в этом сценарии функция потерь является функцией исключительно одной переменной: веса, обозначаемого как w.

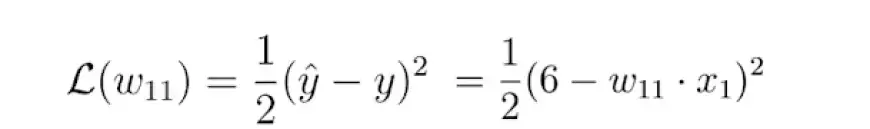
Далее мы вычисляем производную функции потерь по этому параметру:

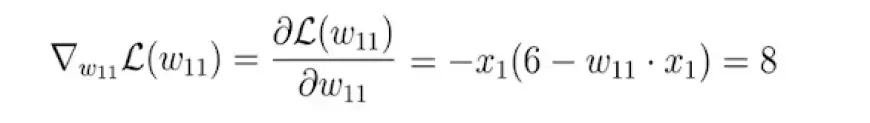
В конечном итоге мы получаем значение 8, которое представляет собой наклон или тангенс функции потерь в соответствующей точке оси X, где находится наш первоначальный вес.

Этот тангенс указывает направление наибольшего увеличения функции потерь и соответствующих весовых параметров по оси x.

По сути, используя градиент функции потерь, мы определили, какие весовые параметры приведут к еще большему значению потерь. Однако наша цель прямо противоположная. Мы можем добиться этого, умножив градиент на -1, получив таким образом обратное направление градиента.

Этот процесс определяет направление наибольшей скорости уменьшения функции потерь и соответствующие параметры вдоль оси x, которые приводят к этому уменьшению:

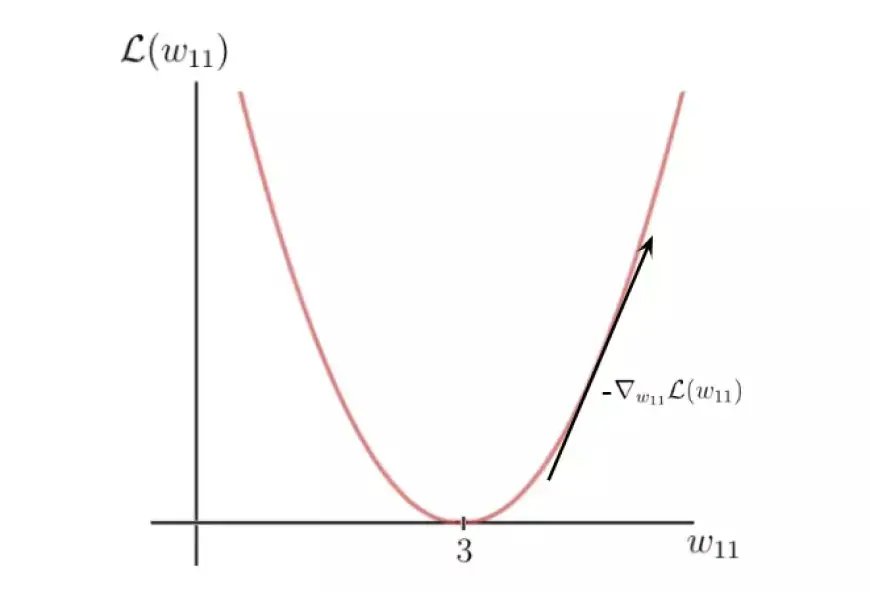
На последнем шаге мы выполняем одну итерацию градиентного спуска, чтобы уточнить наши веса. Используя отрицательный градиент, мы корректируем наш текущий вес в направлении, которое приводит к уменьшению значения функции потерь, как это диктуется отрицательным градиентом:

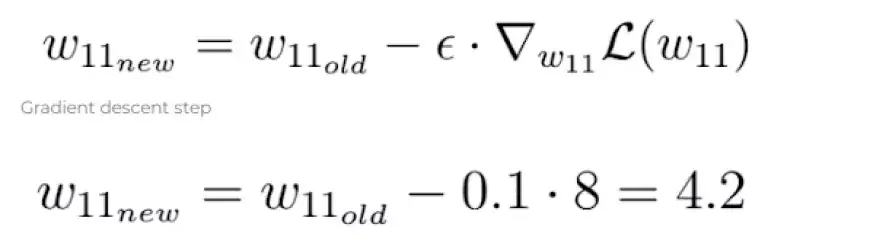
Параметр эпсилон в этом уравнении представляет собой гиперпараметр, известный как скорость обучения. Он определяет скорость, с которой мы корректируем параметры во время оптимизации.

Важно отметить, что скорость обучения — это скалярная величина, с помощью которой мы масштабируем отрицательный градиент, и обычно она остается относительно небольшой. В нашем случае скорость обучения установлена ​​на уровне 0,1.

Как показано, после выполнения шага градиентного спуска наш вес w теперь равен 4,2, что приближает его к оптимальному весу по сравнению с предыдущим значением.

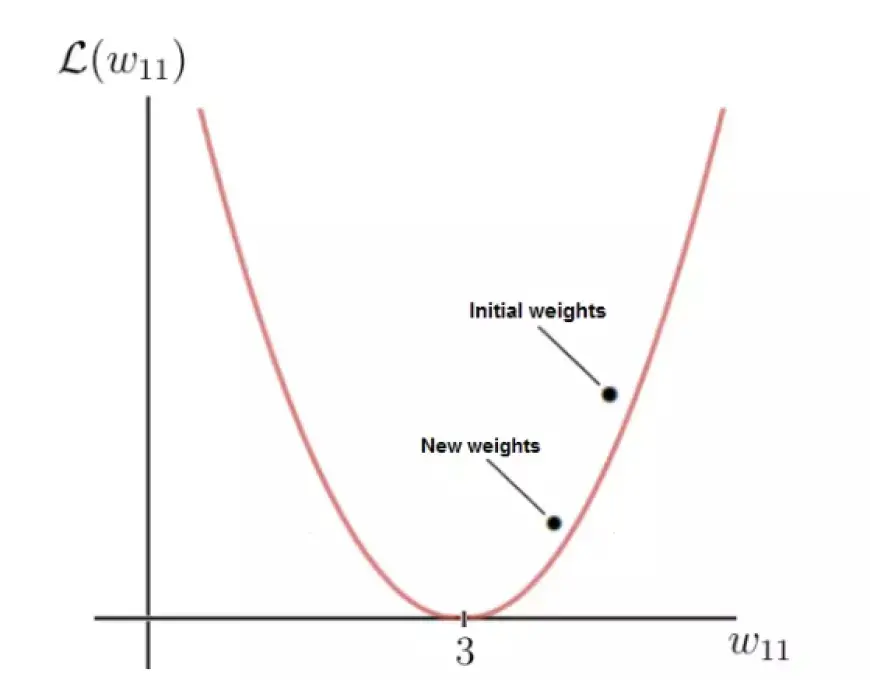
Уменьшенное значение функции потерь для обновленного веса указывает на улучшение, подразумевая, что нейронная сеть теперь более способна делать точные прогнозы. Мысленно выполнив расчет, вы заметите, что новый прогноз действительно ближе к метке, чем раньше.

С каждым обновлением веса мы спускаемся по отрицательному градиенту, постепенно приближаясь к оптимальным весам. После каждой итерации градиентного спуска текущие веса сети сходятся все ближе и ближе к оптимальным весам, что в конечном итоге позволяет нейронной сети делать желаемые прогнозы.